2013년08월18일 68번
[사회통계] 단순회귀모형 Yi=α + βxi + εi(i=1, 2, …, n)에서 잔차 ei=yi-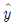 의 성질을 모두 짝지은 것은?
의 성질을 모두 짝지은 것은?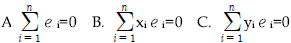
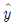 의 성질을 모두 짝지은 것은?
의 성질을 모두 짝지은 것은?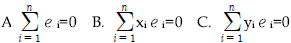
- ① A, B
- ② A, C
- ③ B, C
- ④ A, B, C
(정답률: 20%)
문제 해설




연도별
- 2021년08월14일
- 2021년03월07일
- 2020년09월26일
- 2020년08월22일
- 2020년06월06일
- 2019년08월04일
- 2019년04월27일
- 2019년03월03일
- 2018년08월19일
- 2018년04월28일
- 2018년03월04일
- 2017년08월26일
- 2017년05월07일
- 2017년03월05일
- 2016년08월21일
- 2016년05월08일
- 2016년03월06일
- 2015년08월16일
- 2015년05월31일
- 2015년03월08일
- 2014년08월17일
- 2014년05월25일
- 2014년03월02일
- 2013년08월18일
- 2013년06월02일
- 2013년03월10일
- 2012년08월26일
- 2012년03월04일
- 2011년08월21일
- 2011년03월20일
- 2010년07월25일
- 2010년03월07일
- 2009년07월26일
- 2008년07월27일
- 2008년03월02일
- 2007년08월05일
- 2006년08월06일
- 2005년08월07일
- 2004년08월08일
- 2003년08월10일
- 2003년03월16일
- 2002년08월11일
- 2002년03월10일
- 2001년09월23일
- 2000년09월20일
- 2000년03월12일
진행 상황
0 오답
0 정답
A. 잔차의 합은 0이다. (∑ei=0)
B. 잔차의 평균은 0이다. (mean(ei)=0)
C. 잔차의 분산은 일정하다. (Var(ei)=σ2)
A는 회귀선이 데이터의 중심을 지나기 때문에 성립한다. B는 회귀선이 데이터의 평균을 예측하기 때문에 성립한다. C는 회귀선이 모든 데이터를 완벽하게 설명하지 못하기 때문에 잔차의 분산이 일정하다는 가정을 하고 회귀분석을 수행한다. 따라서 정답은 "A, B"이다.